วิธีสยาม

วิธีสยาม หรือวิธีเดอ ลา ลูแบร์ (อังกฤษ: Siamese method , De la Loubère method) เป็นวิธีการง่าย ๆ ในการสร้างจัตุรัสกล (จัตุรัสตัวเลขซึ่งผลรวมของทุกแถว คอลัมน์ และทแยงมุมมีค่าเท่ากัน) ที่มีความกว้างและยาวเป็นจำนวนคี่ใด ๆ วิธีการดังกล่าวถูกนำสู่ฝรั่งเศสในปี ค.ศ. 1688 โดยนักคณิตศาสตร์และทูตชาวฝรั่งเศส ซีมง เดอ ลา ลูแบร์ เมื่อเขาเดินทางกลับประเทศหลังการเดินทางมาเป็นคณะทูตที่ราชอาณาจักรสยามเมื่อปี ค.ศ. 1687 วิธีสยามทำให้การสร้างจัตุรัสกลเป็นไปอย่างตรงไปตรงมา

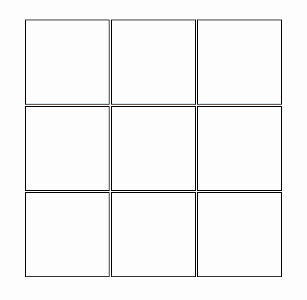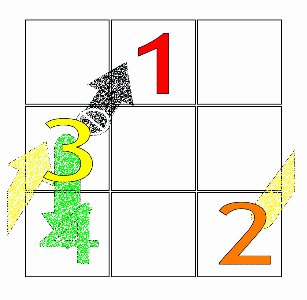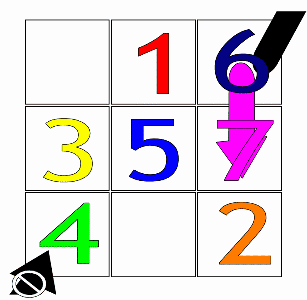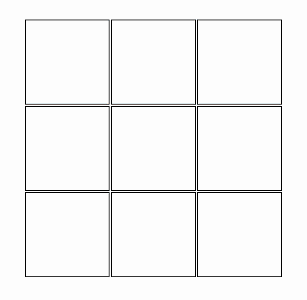ตัวอย่างอย่างง่ายของวิธีสยาม: เริ่มต้นจากช่องกลางแถวแรกด้วยหมายเลข 1 จากนั้นเติมตัวเลขในแนวทแยงขึ้นขวา (↗) ไปทีละช่อง หากทแยงขึ้นไปแล้วจะตกจัตุรัส ให้พับไปยังแถวสุดท้ายหรือคอลัมน์แรกตามลำดับ และหากเติมทแยงแล้วไปเจอช่องที่เติมตัวเลขไว้แล้ว ให้เติมช่องที่อยู่ต่ำลงมาหนึ่งช่อง (↓) แทน จากนั้นจึงเติมตัวเลขต่อไปตามวิธีเดิม

วิธีการ

คำบรรยายวิธีสยามในหนังสือ A new historical relation of the kingdom of Siam โดยซีมง เดอ ลา ลูแบร์

ขั้นแรก จำเป็นต้องเลือกลำดับเลขคณิตขึ้นมาเสียก่อน (ตัวอย่างง่าย ๆ เช่น ลำดับเลขคณิต 1,2,3,4,5,6,7,8,9 สำหรับจัตุรัสขนาดสามคูณสาม)

จากนั้น เริ่มต้นจากช่องกลางของแถวแรกด้วยหมายเลข 1 (หรือตัวเลขแรกของลำดับเลขคณิตใด ๆ ที่เลือกมา) หัวใจของวิธีการในการเติมตัวเลขในช่องทั้งหมดคือการเติมตัวเลขในแนวทแยงขึ้นขวา (↗) ไปทีละช่อง หากทแยงขึ้นไปแล้วจะตกจัตุรัส ให้พับไปยังแถวสุดท้ายหรือคอลัมน์แรกตามลำดับ

หากเติมทแยงแล้วไปเจอช่องที่เติมตัวเลขไว้แล้ว ให้เติมช่องที่อยู่ต่ำลงมาหนึ่งช่อง (↓) แทน จากนั้นจึงเติมตัวเลขต่อไปตามวิธีเดิม

จัตุรัสกลขนาด 3 คูณ 3

step 1
	1
	.
	.

step 2
	1
	.
		2

step 3
	1
3
		2

step 4
	1
3
4		2

step 5
	1
3	5
4		2

step 6
	1	6
3	5
4		2

step 7
	1	6
3	5	7
4		2

step 8
8	1	6
3	5	7
4		2

step 9
8	1	6
3	5	7
4	9	2

จัตุรัสกลขนาด 5 คูณ 5

Step 1
		1
		.
		.
		.
		.

Step 2
		1
		.
		.
		.		3
		.	2

Step 3
		1
	5
4		.
				3
			2

Step 4
		1	8
	5	7
4	6	.
				3
			2

Step 5
		1	8	15
	5	7	14
4	6	13
10	12			3
11			2	9

Step 6
17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9