ทรีพ
ทรีพ (อังกฤษ: Treap) เป็นต้นไม้ค้นหาแบบทวิภาคประเภทหนึ่ง ที่มีการประกันความสูง เฉลี่ยเป็น O (log n) โดยวิธีการนำแนวคิดเรื่องของฮีป เข้ามาช่วย โดยคำว่าทรีพ (treap) นั้นเป็นคำที่เกิดจากการประกอบของคำว่า binary search tree รวมกับคำว่า heap เป็น treap นั้นเอง
| ทรีพ (treap) | |
|---|---|
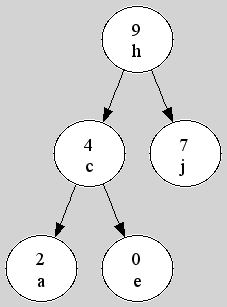 การจัดเรียงข้อมูลตัวอักษรแบบทรีพ โดยใช้ข้อมูลเสริมในลักษณะการเรียงของฮีปมากสุด | |
| ความสำคัญของลำดับ | เรียงจากน้อยไปมาก |
| การซ้ำกันของสมาชิก | อนุญาตให้ซ้ำได้ |
| เวลาที่ใช้ค้นหาตามดัชนี | - |
| เวลาที่ใช้ค้นหาตามค่า | O (log n) |
| เวลาที่ใช้ในการเข้าถึง | O (log n) |
| การทำให้ว่าง | ทำให้รากเป็น null |
| เวลาที่ใช้ทำให้ว่าง | O (1) |
| โครงสร้างต้นแบบ | ต้นไม้ค้นหาแบบทวิภาค |
| โครงสร้างที่นำไปใช้ | - |
ประวัติของการคิดค้นทรีพ
แก้ทรีพถูกคิดค้นโดย Cecilia R. Aragon และ Raimund G. Seidel ในปี 1989 เนื่องจากการสร้างข้อมูลเสริมแบบสุ่ม ทรีพ จึงมีอีกชื่อหนึ่งว่า randomized binary search tree หรือ RBST
ลักษณะของทรีพ
แก้ปมของต้นไม้ทรีพนอกจากจะมีการเก็บข้อมูลหลักแล้ว จะมีการเก็บข้อมูลเสริม ซึ่งได้มาจากการสุ่มจำนวนจริงขึ้นมา โดยเมื่อมองจากข้อมูลเสริมของต้นไม้ทรีพ จะมีลักษณะการเรียงแบบฮีป กล่าวคือปมพ่อจะมีลำดับความสำคัญมากกว่า ปมลูกทั้งสองข้าง การจัดเรียงแบบนี้จะช่วยประกันได้ว่า ความสูงของต้นไม้จะ เตี้ยที่สุดเท่าที่ทำได้ หรือเป็น O (log n)
จุดเด่นของทรีพ
แก้จุดเด่นของทรีพคือการประกันว่าความสูงของต้นไม้จะ เตี๊ยที่สุดเท่าที่ทำได้ หรือเป็น O (log n) โดยสมบัตินี้เกิดการสุ่มที่มีการกระจายแบบฮาร์โมนิก คือ การกระจายที่เท่าๆกัน ส่งผลให้การเรียงเลขที่เกิดจากการสุ่มขึ้นมาเป็นฮีป จะทำให้ต้นไม้อยู่ ในรูปร่างเตี้ยที่สุดได้
บริการที่มักจะมี
แก้- การเพิ่ม ลบ ค้นหาข้อมูลอย่างรวดเร็ว
ความเร็วที่ใช้ในการทำงาน
แก้จุดมุ่งหมายของทรีพจะเน้นการเข้าถึงข้อมูลอย่างรวดเร็ว เนื่องจากสร้าง เป็นต้นไม้ที่ประกันความสูงเป็น O (log n)
ประเภทข้อมูลที่ใช้สร้างทรีพ
แก้ปมของต้นไม้ทรีพแตกต่างจาก ปมของต้นไม้ค้นหาแบบทวิภาค ตรงที่เก็บตัวแปรเพิ่มเป็นจำนวนจริงหนึ่งตัว ซึ่งถูกสุ่มค่าขึ้นมาตั้งแต่ตอนสร้างปม ข้อมูลเสริมส่วนนี้จะใช้ในการเปรียบเทียบเพื่อใช้ในการเรียงโครงสร้างของทรีพ เมื่อมองเฉพาะข้อมูลเสริมจะมีความสัมพันธ์แบบฮีป
การสร้างบริการของทรีพ
แก้การเพิ่มสมาชิก
แก้ขั้นตอนของการเพิ่มข้อมูล จะเพิ่มโดยเหมือนการเพิ่มต้นไม้ค้นหาแบบทวิภาคทุกประการ แต่หลังจากเพิ่มเสร็จแล้วจะทำการเปรียบเทียบข้อมูลเสริมของปมที่เพิ่มว่ามีมีความสำคัญมากกว่าปมพ่อหรือไม่ ที่มีความสำคัญ จะทำการหมุนปมพ่อลงมา และหมุนปมพ่อลงไปเรื่อยๆ จนกว่า ปมพ่อของปมที่เพิ่งเพิ่มมาจะมีความ สำคัญมากกว่า ซึ่งตรงกับนิยามของฮีป การหมุนปมจะทำให้ความสัมพันธ์แบบต้นไม้ค้นหาแบบทวิภาค ที่ข้อมูลในต้นไม้ย่อยด้านซ้ายน้อยกว่าราก และข้อมูลในต้นไม้ย่อยด้านขวามากกว่าราก ยังไม่เสียไป
การลบสมาชิก
แก้ขั้นตอนการลบสมาชิกนั้นทำได้โดยการหมุนปมที่อยากจะลบให้เป็นใบก่อน แล้วจึงลบใบทิ้ง โดยการทำให้เป็น null
การค้นหาสมาชิก
แก้การค้นหาสมาชิกทำได้เหมือนต้นไม้ค้นหาแบบทวิภาคทั่วไป