เคิร์ล

ใน แคลคูลัสเวกเตอร์ เคิร์ล (อังกฤษ: curl) เป็นตัวดำเนินการเวกเตอร์ ที่อธิบาย การหมุนของสนามเวกเตอร์ ในสามมิติ เคิร์ลของแต่ละจุดในสนามแทนด้วยเวกเตอร์ ซึ่งมีคุณลักษณะ (ความยาวและทิศทาง) ที่แสดงถึงลักษณะการหมุนที่จุดนั้น

ทิศทางของเคิร์ลคือแกนของการหมุนตามที่กำหนดโดยกฎมือขวา และขนาดของเคิร์ลคือขนาดของการหมุน เช่น ถ้าสนามเวกเตอร์แทน ความเร็วการไหลของของไหลที่กำลังเคลื่อนที่แล้วเคิร์ลจะเป็นความหนาแน่นของการไหลเวียน ของของไหล สนามเวกเตอร์ที่เคิร์ลเป็นศูนย์ เรียกว่าไร้การหมุน (irrotational) เคิร์ลเป็นรูปแบบของ อนุพันธ์สำหรับสนามเวกเตอร์ โดยรูปทั่วไปของทฤษฎีบทพื้นฐานของแคลคูลัสที่ใช้กับเคิร์ล คือ ทฤษฎีบทของสโตกส์ ซึ่งเชื่อมโยงปริพันธ์ตามผิวของเคิร์ลของสนามเวกเตอร์กับ ปริพันธ์ตามเส้นของสนามเวกเตอร์รอบเส้นโค้งขอบเขตของพื้นผิวนั้น

สัญกรณ์ของเคิร์ล เขียนเป็น curl F หรือ ∇ × F ซึ่งใช้ตัวดำเนินการเดลและผลคูณไขว้ บางครั้งอาจเรียกเคิร์ลว่า โรเตชัน (rotation) หรือ โรเตชันนอล (rotational) เขียนเป็นสัญกรณ์ว่า rot F

เคิร์ลแตกต่างจากตัวดำเนินการเกรเดียนต์และไดเวอร์เจนซ์ เนื่องจากการประยุกต์สู่มิติอื่น ๆ ยากกว่า โดยมีความเป็นไปได้บางวิธี แต่จะมีเพียงในสามมิติเท่านั้นที่เคิร์ลของสนามเวกเตอร์จะเป็นสนามเวกเตอร์เหมือนเดิม ปรากฏการณ์นี้คล้ายกับ ผลคูณไขว้ ซึ่งนิยามในสามมิติและขยายไปใช้ในมิติอื่นได้ยากเช่นเดียวกัน ความสัมพันธ์นี้สะท้อนในสัญกรณ์ ∇× สำหรับเคิร์ล

ชื่อ "เคิร์ล" เสนอเป็นครั้งแรกโดย เจมส์ เคลิร์ก แมกซ์เวลล์ ใน ค.ศ. 1871 แต่แนวคิดนี้มีการใช้งานตั้งแต่ ค.ศ. 1839 ในทฤษฎีสนามเชิงแสงของเจมส์ แมกคัลลัค

องค์ประกอบของ F ที่ตำแหน่ง r ในทิศปกติและทิศสัมผัสกับเส้นโค้งปิด C ในระนาบแบน ที่ล้อมรอบพื้นที่เชิงเวกเตอร์ A = An̂

นิยาม

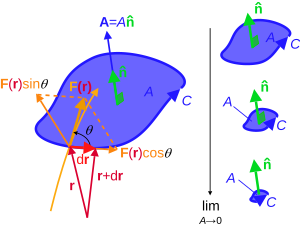
เคิร์ลของสนามเวกเตอร์ F (แทนด้วย curl F หรือ ∇ × F หรือ rot F) ที่จุดหนึ่ง ๆ นิยามจากภาพฉายของมันลงบนเส้นต่าง ๆ ที่ผ่านจุดนั้น ถ้า n̂ เป็นเวกเตอร์หนึ่งหน่วยใด ๆ ภาพฉายของเคิร์ลของ F ไปบน n̂ นิยามโดยลิมิตของปริพันธ์ตามเส้นปิดในระนาบที่ตั้งฉากกับ n̂ หารด้วยพื้นที่ที่ถูกล้อมรอบ เมื่อเส้นทางการหาปริพันธ์ลดขนาดลงสู่จุด

ตัวดำเนินการเคิร์ลนำฟังก์ชันที่หาอนุพันธ์ได้อย่างต่อเนื่อง f : ℝ³ → ℝ³ ไปสู่ฟังก์ชันต่อเนื่อง g : ℝ³ → ℝ³ และโดยทั่วไปแล้วจะแปลงฟังก์ชัน C^kใน ℝ³ เป็นฟังก์ชัน C^k−1 ใน ℝ³

แบบแผนสำหรับการวางแนวเวกเตอร์ของปริพันธ์ตามเส้น

โดยปริยาย นิยามของเคิร์ล เขียนเป็นสมการได้เป็น

$(\nabla \times \mathbf {F} )(p)\ {\overset {\underset {\mathrm {def} }{}}{=}}\lim _{A\to 0}\left({\frac {1}{|A|}}\oint _{C}\mathbf {F} \cdot d\mathbf {r} \right)\mathbf {\hat {n}}$

โดยที่ ∮_C F ⋅ dr คือ อินทิกรัลตามเส้น ตามขอบเขตของพื้นที่รอบจุดและ |A| คือขนาดของพื้นที่ ถ้า n̂ เป็นเวกเตอร์หนึ่งหน่วยที่ตั้งฉากกับระนาบ และ v̂ เป็นเวกเตอร์ปกติที่ในระนาบที่ชี้ออกไปด้านนอกพื้นที่ (ดูภาพขวา) แล้ว ทิศทางของ C จะเลือกให้เวกเตอร์สัมผัส ω̂ ของ C ทำให้ {n̂,ν̂,ω̂} เป็นชุดเวกเตอร์ที่เป็นไปตามกฎมือขวา

การใช้งาน

ในทางปฏิบัติ นิยามข้างต้นไม่ค่อยได้ใช้เพราะในเกือบทุกกรณี ตัวดำเนินการเคิร์ลสามารถนำมาใช้ในกรอบของระบบพิกัดเชิงเส้นโค้งบางระบบ ที่มีการคำนวณหาสูตรที่ง่ายกว่าเอาไว้แล้ว

สัญกรณ์ ∇ × F มีต้นกำเนิดในความคล้ายคลึงกับผลคูณไขว้สามมิติ และมีประโยชน์ในการช่วยจำสูตรหาเคิร์ลในระบบพิกัดคาร์ทีเซียน โดย ∇ แทนตัวดำเนินการเดล สัญกรณ์เช่นนี้ถือเป็นปกติใน ฟิสิกส์ และ พีชคณิต

เมื่อกระจายสูตร ∇ × F ในระบบพิกัดคาร์ทีเซียนสามมิติ (ดู เดลในพิกัดทรงกระบอกและทรงกลม สำหรับสูตรในระบบพิกัดทรงกลม และทรงกระบอก พิกัด) สำหรับ F ที่มีองก์ประกอบเวกเตอร์เป็น [F_x, F_y, F_z] จะได้เป็น

${\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\[5pt]{\dfrac {\partial }{\partial x}}&{\dfrac {\partial }{\partial y}}&{\dfrac {\partial }{\partial z}}\\[10pt]F_{x}&F_{y}&F_{z}\end{vmatrix}}$

โดยที่ i, j, และ k เป็น เวกเตอร์หน่วย สำหรับ แกน x y และ z ตามลำดับ สิ่งนี้จะขยายออกดังนี้:

$\left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right)\mathbf {k}$

แม้ว่าจะแสดงในรูปแบบของพิกัด ผลลัพธ์นี้จะไม่เปลี่ยนแปลงภายใต้การหมุนที่เหมาะสมของแกนพิกัด แต่จะพลิกด้านภายใต้การสะท้อน