รูปวงรี

วงรี (อังกฤษ: ellipse) เป็นเส้นโค้งทางคณิตศาสตร์ซึ่งล้อมรอบจุดโฟกัสสองจุดและทำให้ผลรวมของระยะทางจากจุดบนเส้นโค้งไปหาจุดโฟกัสแต่ละจุดเป็นค่าคงที่ จากนิยามนี้ วงรีถือเป็นนัยทั่วไปของวงกลม นั่นคือ วงกลมเป็นกรณีพิเศษของวงรีที่มีจุดโฟกัสซ้อนกันเป็นจุดเดียว ความยืดของวงรีแสดงด้วยค่าความเยื้องศูนย์กลาง ซึ่งสำหรับวงรีอาจมีค่าได้ตั้งแต่ 0 (กรณีพิเศษของวงกลม) และมากเข้าใกล้ 1 เท่าใดก็ได้ แต่ไม่ถึง 1 (ซึ่งจะกลายเป็นพาราโบลา) วงรียังสามารถนิยามเป็นเซตของจุด ที่สำหรับแต่ละจุดในเซต อัตราส่วนของระยะทางไปหาจุดที่กำหนด(ซึ่งจะเป็นหนึ่งในจุดโฟกัส)ต่อระยะทางไปหาเส้นที่กำหนด(เรียกว่าเส้นไดเรกทริกซ์) เป็นค่าคงที่ ซึ่งค่าคงที่นี้จะเท่ากับความเยื้องศูนย์กลางข้างต้น

วงรีซึ่งมาจากการตัดของทรงกรวยกับระนาบ

นิยามสองแบบของวงรีซึ่งเทียบเท่ากัน: ใช้โฟกัสสองจุด(เขียว) และใช้โฟกัสกับไดเรกทริกซ์(น้ำเงิน)

วงรีเป็นภาคตัดกรวย นั่นคือ เกิดจากการตัดกันของทรงกรวยกับระนาบ (ดูภาพขวา) และยังเป็นภาคตัดของทรงกระบอก ยกเว้นเฉพาะกรณีที่ระนาบตัดขนานกับแกนทรงกระบอก

นิยาม

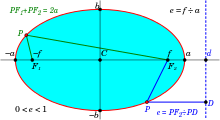
วงรีมักนิยามเป็นโลกัสของจุดในระนาบสองมิติ โดยจากจุดโฟกัส $F_{1}$กับ $F_{2}$และระยะทาง $2a$จะนิยามวงรีเป็นเซตของจุด $P$ทั้งหมดที่ทำให้ผลบวกของระยะทาง $|PF_{1}|$กับ $|PF_{2}|$เป็น $2a$หรือเขียนเป็นสัญกรณ์ว่า $E=\{P\in \mathbb {R} ^{2}|\ |PF_{1}|+|PF_{2}|=2a\}$(กรณีที่ $2a\leq |F_{1}F_{2}|$จะลดรูปเป็นเส้นตรง ดังนั้นเพื่อให้เป็นวงรีจะต้องบังคับ $2a>|F_{1}F_{2}|$)

จุดกึ่งกลางของส่วนของเส้นตรงเชื่อมจุดโฟกัสทั้งสอง เรียกว่าจุดศูนย์กลางของวงรี เส้นตรงที่ผ่านจุดโฟกัสทั้งสองเรียกว่าแกนเอก และเส้นที่ผ่านจุดศูนย์กลางและตั้งฉากกับแกนเอกเรียกว่าแกนโท แกนเอกตัดกับวงกลมที่จุดยอด ซึ่งห่างจากจุดศูนย์กลาง $a$ หน่วย ระยะทางจากจุดโฟกัสไปจุดศูนย์กลางเรียกว่าระยะโฟกัส $c$ อัตราส่วน ${\tfrac {c}{a}}=e$ คือความเยื้องศูนย์กลาง

สมบัติ

ในระบบพิกัดคาร์ทีเซียน วงรีที่มีจุดศูนย์กลางที่ $(h,k)$ แกนเอกขนานแกน x ยาว $2a$ แกนโทขนานแกน y ยาว $2b$ เขียนสมการได้เป็น:

${\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1$

ความเยื้องศูนย์กลางของวงรีเป็นไปตามสูตร

$e={\sqrt {1-\left({\frac {b}{a}}\right)^{2}}}$

หากใช้ระบบสมการอิงตัวแปรเสริม จะสามารถเขียนวงรีในรูปของฟังก์ชันตรีโกณมิติเป็น

$x=h+a\cos t,\ y=k+b\sin t,\ 0\leq t<2\pi$

หากแทน $u=tan(t/2)$ จะได้สมการตัวแปรเสริมอีกรูปคือ

$x=h+a\left({\frac {1-u^{2}}{1+u^{2}}}\right),\ y=k+b\left({\frac {2u}{1+u^{2}}}\right),\ -\infty <u<\infty$

ในพิกัดเชิงขั้ว หากใช้จุดศูนย์กลางของวงรีเป็นจุดกำเนิด และวัดมุมเทียบกับแกนเอก จะได้เป็นสมการ

$r(\theta )={\frac {ab}{\sqrt {(b\cos \theta )^{2}+(a\sin \theta )^{2}}}}={\frac {b}{\sqrt {1-(e\cos \theta )^{2}}}}$

แต่หากใช่จุดโฟกัสเป็นจุดกำเนิด จะได้สมการที่ง่ายกว่า คือ

$r(\theta )={\frac {a(1-e^{2})}{1\pm e\cos \theta }}$

วงรีมีพื้นที่ $\pi ab$ เห็นได้จากการมองวงรีเป็นวงกลมรัศมี $b$ที่ถูกยืดออก $a/b$ เท่า จึงได้พื้นที่เป็น $(\pi b^{2})({\frac {a}{b}})=\pi ab$ หรืออาจพิสูจน์จากการอินทิเกรต โดยจัดรูปสมการวงรี ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ เป็น $y=b{\sqrt {1-x^{2}/a^{2}}}$อินทิเกรตจาก $-a$ ถึง $a$ จะได้พื้นที่ครึ่งบน ดังนั้นได้เป็น

${\begin{aligned}A&=2\int _{-a}^{a}b{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\ dx\\&={\frac {b}{a}}\cdot 2\int _{-a}^{a}{\sqrt {a^{2}-x^{2}}}\ dx\\&={\frac {b}{a}}\cdot \pi a^{2}\\&=\pi ab\end{aligned}}$

ความยาวรอบรูปของวงรีไม่สามารถเขียนเป็นสูตรอย่างง่ายได้ โดยมีค่าเท่ากับอินทิกรัล

$C=4a\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta =4aE(e)$

เมื่อ $E$ เป็นปริพันธ์วงรีสมบูรณ์ชนิดที่สอง (Complete elliptic integral of the second kind)

$E(e)=\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta$

สูตรความยาวรอบรูปสามารถเขียนในรูปอนุกรมอนันต์ได้เป็น

${\begin{aligned}C&=2\pi a\left[{1-\left({\frac {1}{2}}\right)^{2}e^{2}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {e^{4}}{3}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}{\frac {e^{6}}{5}}-\cdots }\right]\\&=2\pi a\left[1-\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}}\right]\end{aligned}}$

รามานุจันได้ให้สูตรประมาณค่าความยาวรอบรูปว่า

$C\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]=\pi \left[3(a+b)-{\sqrt {10ab+3(a^{2}+b^{2})}}\right]$